手持ちのスカウト産☆4,5が育成し終えたこともあり、メダルが徐々にあまり始めてきました!
そのまま取っておいても勿体無いので、メダルロトリーの検証に使ってみました!今回は4000連分までですが、目指せ10000連分のデータということでメダルが貯まり次第追加でロトリーチャレンジしてきます!
結果
集計結果
6000連分(10連×600)の結果になります。
| アイテム分類 | アイテム名前 | 頻度[回] |
|---|---|---|
| 進化素材 (4340) | 花セット | 1450 |
| 蕾セット | 1408 | |
| 種セット | 1482 | |
| 覚醒の書 (876) | ☆5書 | 56 |
| ☆4書 | 77 | |
| ☆3書 | 190 | |
| ☆2書 | 553 | |
| 強化用ルーン (393) | 33.000 | 1 |
| 32.000 | 2 | |
| 31.000 | 8 | |
| 30.000 | 18 | |
| 29.000 | 58 | |
| 28.000 | 79 | |
| 27.000 | 227 | |
| ユニット (386) | ☆4ユニット | 124 |
| ☆3ユニット | 262 | |
| その他 | 古代のルーン石 | 5 |
動画データ
動画データをいつものように埋め込むとページの読み込みに影響が出そうなのでYoutubeへのリンクを貼っておきます。
メダルロトリー2000連(3セット目)
5セットできれば10000連でキリが良いのですがメダルが足りぬ……。
確率の考察
めっちゃ統計の話になっちゃいましたが!一応!確率の考察!
メルストのメダルロトリーを例にちょっとだけ基礎知識をば!
多少の知識がないとこのトグルの下の内容がわからなくなりそうなので……。数式は省けるだけ省いたよ!言葉のニュアンスだけでも!
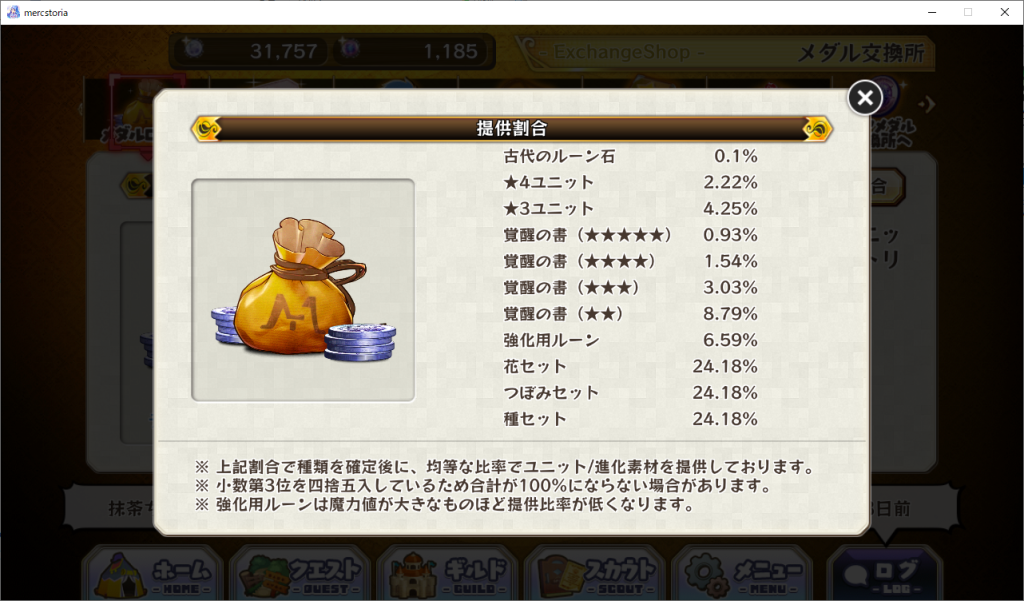
まず最初にメダルロトリーの各アイテムの提供割合(画像1)を元に確率についての基本を確認してみます。
●確率の約束事
まず大前提として確率には3つの暗黙の了解があります。
- すべて事象の確率を足すと1(100%)になる。
- どの事象の確率も0(0%)未満になることはないし、1(100%)を超えることもない。
- それぞれ独立した事象があったとき、『AまたはBが起こる確率』は『Aが起こる確率とBが起こる確率の和』に等しくなる。
1と2については説明が不要だと思うので3について少し具体的なイメージで捕捉をしておくと、単発のメダルロトリーにおいて花セットが出る確率は24.18%で蕾セットが出る確率は24.18%です。このロトリーを1回引いた時、花セットか蕾セットのどちらかが出る確率は48.36%になりますよね?という話です(1回の抽選でこの2つが同時に出ることはあり得ないためです)。
●古代のルーン石を例に考える確率
上記の約束事項(公理)を抑えたうえで、例として古代のルーン石の確率について考えてみます。
まず1000連以内に古代のルーン石が1つ以上獲得できる確率はどのくらいかという問題についてみていきます。
1回だけ引いて出る確率は明記されている通り0.001(0.1%)なので、逆に外れる確率は0.999(99.9%)になります。1000連までずーっと外れを引き続ける確率は0.999(99.9%)を1000回連続で引き続ける確率に相当するので、1000連で古代のルーン石をひけない確率は0.9991000≒0.368(36.8%)になります。なので100人のプレイヤーが1000連分引いても37人くらいは古代のルーン石が1個もでない感じになるわけですね。
単純に確率0.1%という数字を見ると、『1000連引けば出る!』という風に安易にとらえがちな確率ですが、実際はこんな感じです(画像2)。ちなみに2000連時点でも86.5%という確率に……。
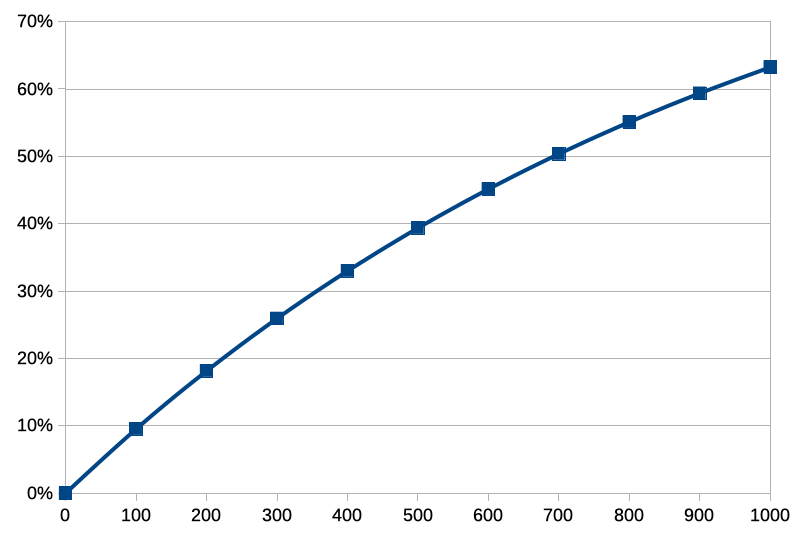
x連までに古代のルーン石を1個以上引ける確率をy%として書いたグラフ
●確率分布
メルストのメダルロトリーの確率分布は下の画像のようになっています(画像3)。画像1と見比べてもらえばなんとなくわかってもらえると思います。
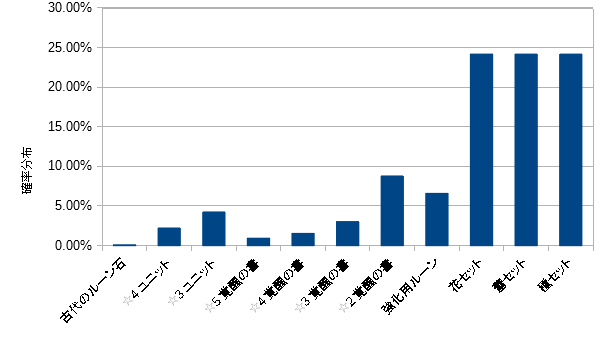
この確率分布は一様分布とか正規分布とか二項分布になっていないのでそのままでは議論できません。そこで標本分布というものを考えます。
●標本分布
標本分布について考える前に標本について述べておきます。標本というのは母集団から抽出したデータの事でメルストのメダルロトリーで例えるなら、母集団はメダルロトリーの中に入っている無限のアイテムに相当し、標本に該当するのは引いたときに出てきたアイテムになります。
標本として取り出されたデータに対して平均をとったものを標本平均と呼びます(ちなみに母集団の平均を母平均と呼びます)。抽出したデータから求めた平均と母集団の平均ではどうしても誤差が出てきます。というのも標本平均というのは取り出された標本次第で変わってきますよね?この標本平均の分布を考えるのが標本分布に当たります。
実はこの標本分布は正規分布に従うことが知られています(中心極限定理)。ムズカシイ話はおいといて、標本平均の分布を考えると統計学の十八番の正規分布(画像4)に持ち込めるので母集団の推定や検定が行えるようになるのです!(とにかく便利ダヨ)
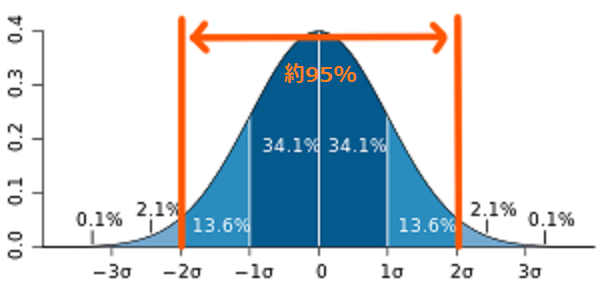
約95%のデータは平均±2σの範囲に収まるという図
●大数の法則と標本サイズ
さっきのところで標本分布を考えるよという話をしましたが、標本抽出がそもそも1セットしかできない場合はどうするのでしょう。例えばメルストのダイヤスカウトはお高いので微課金勢には『100連のデータを10セットとる』みたいなことは無理です、破産します。そんなときに出てくるのが大数の法則です。
名前の通り沢山のデータ(標本)を集めると、標本平均が母平均に近づいていくことが期待されるみたいな法則になります。これは感覚的にもわかると思います。『10回のスカウトの結果より、100回スカウトした結果の方が情報としての信憑性があるよね!』って解釈でオッケーです。
●信頼区間
信頼区間というのは標本のデータから『母集団の平均が〇〇以上××以下に95%の確率で入っている』みたいな事をする統計的手法になります。100回標本から母平均を推定したら95回は当たってるみたいなイメージです。〇〇以上××以下の部分(信頼区間の両端)を信頼限界と呼びます。
今回は信頼区間の推定に正規分布(z分布)を使うよ!
●検定
推測統計学において信頼区間と同じくらい大事な検定です。こちらは帰無仮説と対立仮説をセットで立ててその仮説が棄却できるかどうかを考える話になります。
画像4で見てもらった通り正規分布は両端が狭い感じになってましたよね。標本として採ってきたデータがあの狭いエリアに入ったら珍しいことが起きたな、もしかしたら帰無仮説が間違ってるんじゃないかみたいな議論をすることができます。帰無仮説が間違っているならその反対に位置する対立仮説の可能性があるみたいなやつです。
帰無仮説が棄却できない場合は帰無仮説を受容せざるを得ないので今回のデータでは差は認められなかったという考察になります。ただたまたまそういったデータ群を使ってしまったケースも考えられるのですぐさま差がないと断言することはできない点は注意です。
●信頼区間を計算してみる
まずは母集団の情報(排出率の情報など)が全く無かったものとして得られたデータから特定のアイテムが出る確率の95%信頼区間を求めてみます。標本サイズが十分に大きいのでここではt分布ではなく正規分布を使うことにします。
まずは花セットについて考えてみます。花セットが出たら1点それ以外のアイテムが出たら0点として点数をつけると、4000連したところ949回出たので949点/4000点になります。そのため標本平均は949÷4000=0.23725(23.725%)となります。
正規分布の表から95%信頼区間は0.22406≦μ≦0.25043(22.4%〜25.0%の間に入っている確率が95%という意味)になります(母分散については未知ですが標本サイズが十分に大きいのでt分布と標準分布がほぼほぼ同じになるので標本分散でそのまま代用しています)。
ここで実際の提供割合を見てみると花セットの排出率は24.18%となっており95%信頼区間で推定した範囲に入っているのがわかります。信頼区間は標本サイズの平方根に反比例しているのでデータが増えるほど信頼区間の幅が狭まります!
強化用ルーンの確率がサイズごとに表記されていないので、標本データから95%信頼区間で推定してみると以下の表のようになります。確率がマイナスになっている箇所は標本サイズが十分では無かったために発生しているので気にせず0(0%)以上と置き換えて貰えば大丈夫です。
| 魔力値 | 95%信頼区間(下) | 標本平均 | 95%信頼区間(上) |
|---|---|---|---|
| 33.000 | -11.4% | 0.4% | 12.1% |
| 32.000 | -11.4% | 0.4% | 12.1% |
| 31.000 | -8.8% | 2.5% | 13.9% |
| 30.000 | -6.3% | 4.7% | 15.7% |
| 29.000 | 6.8% | 15.9% | 25.1% |
| 28.000 | 11.0% | 19.6% | 28.1% |
| 27.000 | 50.5% | 56.5% | 62.6% |
●検定をしてみる
信頼区間の推定は提供割合が書いてある時点で、ぶっちゃけやる意味がないです。本題はこっち!
ここでは以下のように仮説を立てます。
- 帰無仮説:提供割合に書かれている確率と実際の確率に差はない
- 対立仮説:提供割合に書かれている確率と実際の確率に差がある
このように仮説を立て、帰無仮説が棄却できるかどうかを考えます。帰無仮説が棄却できれば対立仮説を採択することができます。
今回は古代のルーン石の数が思ったよりも出なかったので、今回の結果が妥当な範囲にあるのかを考えてみます。
- 帰無仮説:『標本データにおける古代のルーン石の確率』と提供割合に書かれている確率に差はない
- 対立仮説:『標本データにおける古代のルーン石の確率』と提供割合に書かれている確率に差がある
まずは標本データに触る前に提供割合から正規分布を書いておきます。以降の議論では有意水準は5%とします。
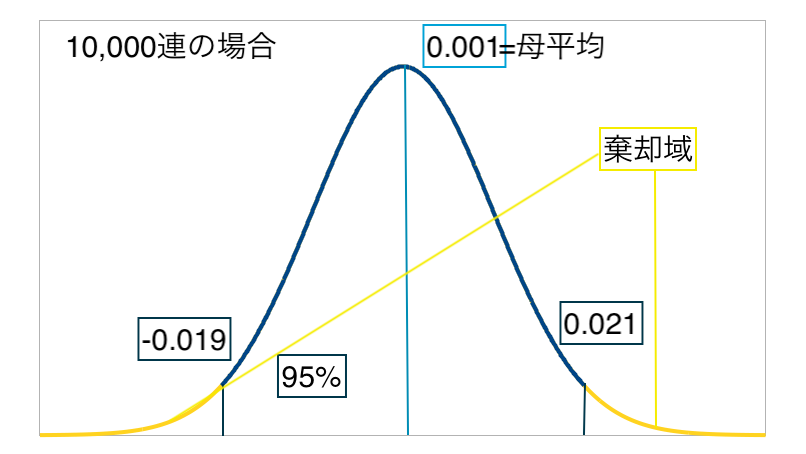
10000連の場合だと標本平均が-0.019(-1.9%)以下又は0.021以上(2.1%)以上にならないと帰無仮説が棄却できないようです。今回は4000連しかデータをとっていないので上図よりも標本サイズが小さいです。標本サイズが小さいと棄却域は母平均から遠くなるので、帰無仮説を棄却するために必要な値もよりシビアになります。
実際に4000連回した結果古代のルーン石が2個出た今回の標本データでは標本平均が0.05%(=0.0005)になるので棄却域には入っていません。そのため帰無仮説を受容せざるを得ないということになります。
ただ今回の場合確率がマイナスになるわけがないので最初から帰無仮説を棄却できなかったわけです。この問題はデータを大量にとることで解消されます。例えば10,000,000連分のデータが取れたと場合、正規分布を書いてみると棄却域の範囲が0.0004(0.04%)以下と0.0016(0.16%)以上になり小さい方の値がマイナスではなくなります。古代のルーン石の確率について本気で議論をする場合はこれくらいのデータを集めないと駄目なのかもしれませんね……。
古代のルーン石の場合は少々確率が低すぎてレアケースになっちゃいましたが、強化用ルーンについて計算してみます。帰無仮説は先ほど同様、母集団の平均と標本平均に有意な差はないという仮説で行きます。
提供割合によると強化用ルーンは6.59%の確率らしいので標本サイズが4000の場合と10000の場合の棄却域を計算して出します。
| 標本サイズ | 棄却域 |
|---|---|
| 4000連 | 0.0379(3.79%)以下or0.0939(9.39%)以上 |
| 10000連 | 0.0482(4.82%)以下or0.0836(8.36%)以上 |
今回の標本データでは4000回中、276回強化用ルーンを引けたので標本平均は0.069(6.9%)となり帰無仮説を棄却できずとなりました。今回の結果からは提供割合に対して逸脱した偏りは見られなかったよという話になります。
長々と書いて分かったことが『今回の結果は提供割合と比べて問題がなかったよ』というのは大変つまらないものですが、一度数学的に確かめてみたかったので計算してみました!

